Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 블록체인 강의
- 우선순위큐
- 디스크블록할당
- 오블완
- Entity
- 자바문자열구분
- 해시
- national instruments
- StringTokenizer
- 자바스크립트
- K-MOOC
- TypeScript
- 머신러닝
- 혁신의기술2:신뢰의미래 블록체인을 만나다
- 시스템프로그래밍
- 자바
- biginteger사용법
- 블록체인
- 자바입력받기
- 딥러닝
- K-MOOC 단국대학교 홍보단
- 컴파일시스템
- stringreader
- html기초
- 2차원배열정렬
- 단국대학교 k-mooc
- Node
- 티스토리챌린지
- 블록체인강의
- CSS 기초
Archives
- Today
- Total
열정 실천
[자료구조] 힙 Heap _ 최대 힙, 최소 힙 (구현 with JAVA) 본문
728x90
힙(Heap)은 우선순위 큐(Priority Queue)를 효율적으로 구현하기 위한 자료구조이다.
우선순위 큐는 큐에서 우선 순위가 높은 순으로 데이터가 나가는 형태로
우선순위를 고려하는 운영체제 스케줄링, 네트워크 패킷 처리 등에 사용된다.
힙은 최댓값과 최솟값을 O(1) 시간에 빠르게 찾을 수 있고,
삽입/삭제 연산도 O(log N)으로 효율적이다.
힙은 완전 이진 트리로 구현되는데, 완전 이진 트리란 왼쪽부터 차례로 채워져 트리의 마지막 레벨을 제외하고 모든 레벨이 꽉 차있는 트리의 구조를 말한다.

힙(Heap)은 최대 힙(Max Heap)과 최소 힙(Min Heap)으로 나뉜다.

최대 힙:
- 부모 노드가 자식 노드보다 크거나 같은 값을 가진다.
- 따라서, 루트 노드는 항상 트리에서 가장 큰 값을 가진다.
최소 힙:
- 부모 노드가 자식 노드보다 작거나 같은 값을 가진다.
- 루트 노드는 항상 트리에서 가장 작은 값을 가진다.
**왼쪽 자식과 오른쪽 자식의 대소 조건은 없다. 부모랑만 비교
삽입(Insert) / 삭제(Delete) 후 힙 재정렬 과정
힙 구현에서는 삽입과 삭제가 발생할 때마다 힙을 재정렬 해주는 것이 핵심 과정이다.
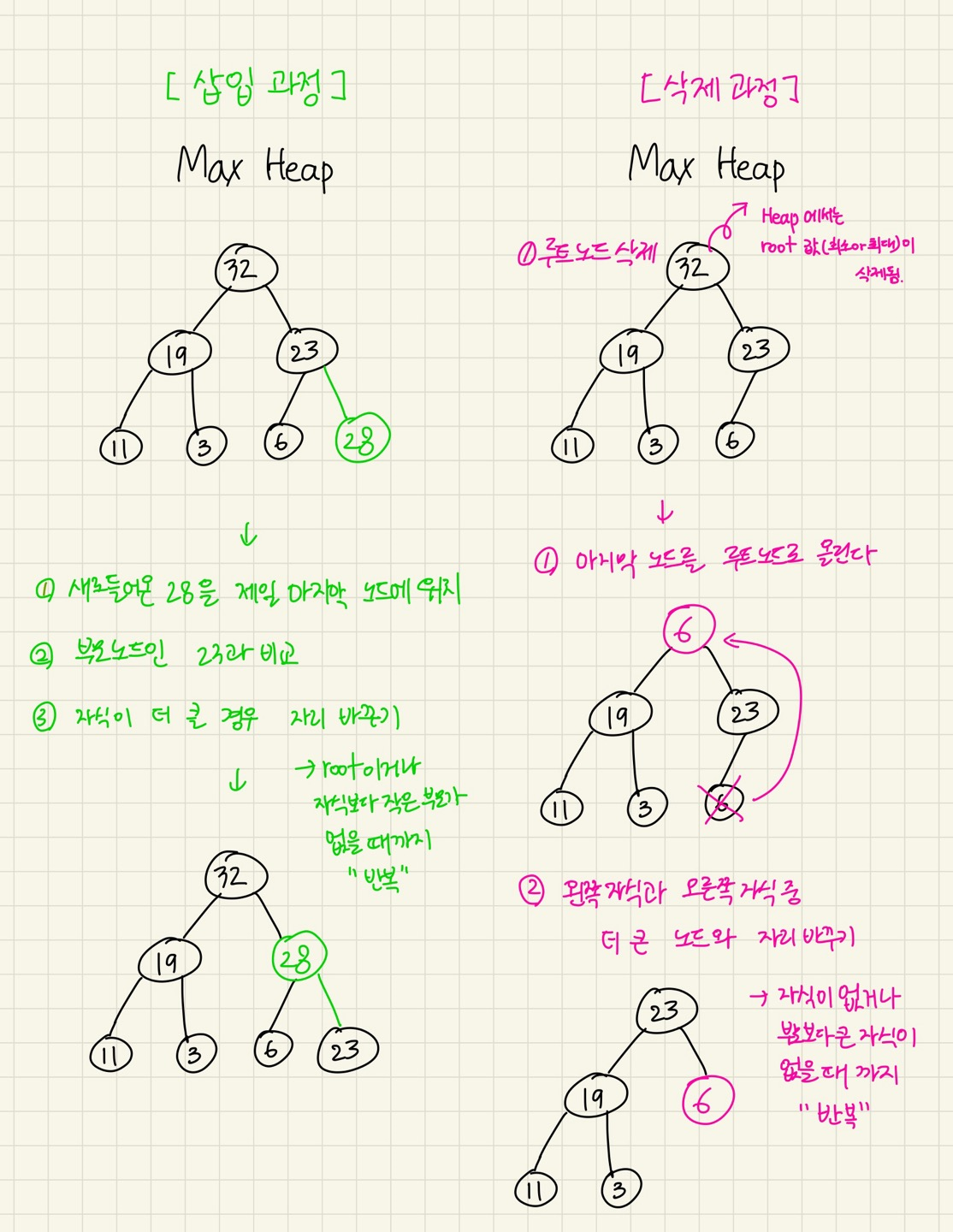
최대 힙 구현
import java.util.ArrayList;
public class MaxHeap {
private ArrayList<Integer> heap;
// 생성자
public MaxHeap(){
heap = new ArrayList<>();
heap.add(0); // 첫 번째 인덱스는 사용하지 않음
}
// 삽입 메소드
public void insert(int val){
heap.add(val); // 새로 추가한 노드 데이터
int cur_index = heap.size() - 1; // 새로 추가한 노드 인덱스 : heap 사이즈 - 1
while(cur_index > 1 && val > heap.get(cur_index / 2)){ // 부모보다 큰지 비교
// 현재 인덱스가 1보다 크고 && 현재 노드 값이 부모노드 값보다 크면
// 현재 노드와 부모 노드 위치 바꾸기
int temp = heap.get(cur_index / 2);
heap.set(cur_index / 2, val);
heap.set(cur_index, temp);
// 노드 인덱스를 부모 인덱스로
cur_index /= 2;
}
}
// 삭제 메소드
public int delete(){
if(heap.size() == 1){
return 0; // 힙이 비어있음
}
// 삭제할 값 == 루트값 == 최댓값
int root = heap.get(1);
// 마지막 노드를 root에 삽입하고 마지막 노드 삭제
heap.set(1, heap.get(heap.size() - 1));
heap.remove(heap.size() - 1);
// 다시 트리 정렬
int cur_index = 1; // root 인덱스
while(cur_index * 2 < heap.size()) { // 자식이 없을 때까지 반복
int leftChild = cur_index * 2;
int rightChild = cur_index * 2 + 1;
// 자식 중 더 큰 값을 선택 (오른쪽 자식이 없으면 왼쪽 자식만 비교)
int largerChild = leftChild;
if(rightChild < heap.size() && heap.get(rightChild) > heap.get(leftChild)) {
largerChild = rightChild;
}
// 부모가 자식보다 크거나 같으면 종료
if(heap.get(cur_index) >= heap.get(largerChild)){
break;
}
// 부모와 더 큰 자식 교환
int temp = heap.get(cur_index);
heap.set(cur_index, heap.get(largerChild));
heap.set(largerChild, temp);
// 현재 인덱스를 자식 인덱스로 변경
cur_index = largerChild;
}
return root;
}
}
최소 힙 구현
import java.util.ArrayList;
public class MinHeap {
private ArrayList<Integer> heap;
//생성자
public MinHeap(){
heap = new ArrayList<>();
heap.add(0); // 첫 번째 인덱스는 사용하지 않음
}
//삽입 메소드
public void insert(int val){
heap.add(val); //새로 추가한 노드 데이터
int cur_index = heap.size()-1; //새로 추가한 노드 인덱스 : heap 사이즈 - 1
while(cur_index>1&&(val< heap.get(cur_index/2))){
//현재 인덱스가 1보다 크거나(부모노드가 있다는 뜻) && 현재 노드 값이 부모노드 값보다 작으면
//현재 노드와 부모 노드 위치 바꾸기
int temp = heap.get(cur_index/2);
heap.set(cur_index/2,val);
heap.set(cur_index,temp);
//노드 인덱스 부모 인덱스로!
cur_index /= 2;
}
}
//삭제 메소드
public int delete(){
if(heap.size()==1){
return 0; // 힙이 비어있음
}
//삭제할 값 == 루트값 == 최솟값
int root = heap.get(1);
//마지막 노드를 root에 삽입하고 마지막 노드 삭제
heap.set(1,heap.get(heap.size())-1);
heap.remove(heap.size()-1);
//다시 트리 정렬
int cur_index=1; //root 인덱스
while( cur_index*2 < heap.size()) { // 자식이 없을 때까지 반복
int leftChild = cur_index*2;
int rightChild = cur_index*2+1;
// 자식 중 더 작은 값을 선택 (오른쪽 자식이 없으면 왼쪽 자식만 비교)
int smallerChild = leftChild;
if(rightChild < heap.size() && heap.get(rightChild) < heap.get(leftChild)) {
smallerChild = rightChild;
}
// 부모가 자식보다 작으면 종료
if(heap.get(cur_index) <= heap.get(smallerChild)){
break;
}
// 부모와 더 작은 자식 교환
int temp = heap.get(cur_index);
heap.set(cur_index, heap.get(smallerChild));
heap.set(smallerChild, temp);
// 현재 인덱스를 자식 인덱스로 변경
cur_index = smallerChild;
}
return root;
}
}

728x90
'CS > DATA STRUCTURE' 카테고리의 다른 글
| [JAVA] Hash 자료구조 / 자바에서 Hashmap 사용하기 (0) | 2024.09.04 |
|---|---|
| C언어 메모리 동적 할당 (0) | 2022.07.06 |
| [자료구조] 알고리즘 성능 분석 - 시간복잡도, 공간복잡도, 빅오표기법 (0) | 2022.06.30 |
| [자료구조] 추상자료형 (0) | 2022.06.29 |
| [자료구조] 시작하기 - 자료구조란? 자료구조의 분류 (0) | 2022.06.29 |


